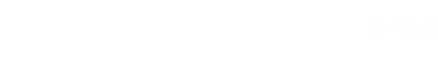Why do reported growth rates differ for the same variable? Refer to the last three years of GDP data to see… [this is an updated version of this 2018 post]
Figure 1: Quarterly GDP, SAAR, FRED series GDPC1 (black line), annual, FRED series GDPCA (blue bars), in billions of Chained 2012$. 2018 annual (quarterly) growth rate (pink arrow); annual 2018 y/y growth rate (orange arrow); 2020Q1 annual quarterly growth rate (red arrow); 2020Q1 q/q SAAR growth rate (green arrow). Source: BEA, 2020Q1 3rd release via FRED, and author’s calculations.
Note: SAAR denotes Seasonally Adjusted at Annual Rates.
Conventions in the US are to cite q/q SAAR or y/y quarterly data (i.e., 4 quarter changes). In Europe, q/q growth rates are typically not annualized.
So, there are several ways to calculate the growth rate over the course of the year. They will almost invariably differ, perhaps substantially, when GDP is either growing very rapidly or shrinking very rapidly. And there is no “right” way. If one wants to calculate the most recent growth experience, one might stress q/q. If one wants to look at a longer horizon, then one might want to use the quarterly y/y. If one thinks quarterly series are very noisy, one might want to look at annual y/y.
Additional Note: One could average the q/q annualized growth rates over the four quarters of 2017 to try to get 2017 q4/q4 growth rate. This calculation leads to an approximation, which gets worse the more variable growth rates are (unless growth rates are calculated as log-differences — which is part of the reason economists like to express variables in logs and log differences…).
By the way, 10% decline combined with a 10% rise does not bring you back where you started — unless you calculate growth rates in logs. Here’s Jim Hamilton‘s take (for some reason, people start calling me names when I try to defend the use of logs.)